请问这样的曲线有标准方程吗？

V2EX = way to explore

V2EX 是一个关于分享和探索的地方

现在注册

已注册用户请登录

这是一个创建于 1031 天前的主题，其中的信息可能已经有所发展或是发生改变。

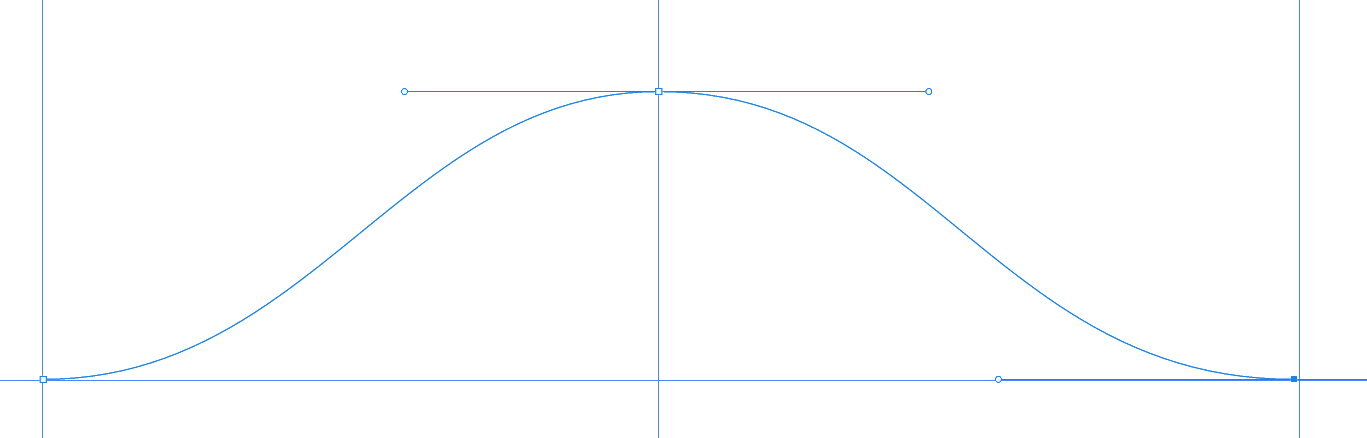
我想做一个 js 动画，知道 x 的值，怎么求 y

第 1 条附言 · 2022-03-04 15:43:34 +08:00

我感觉贝塞尔很接近
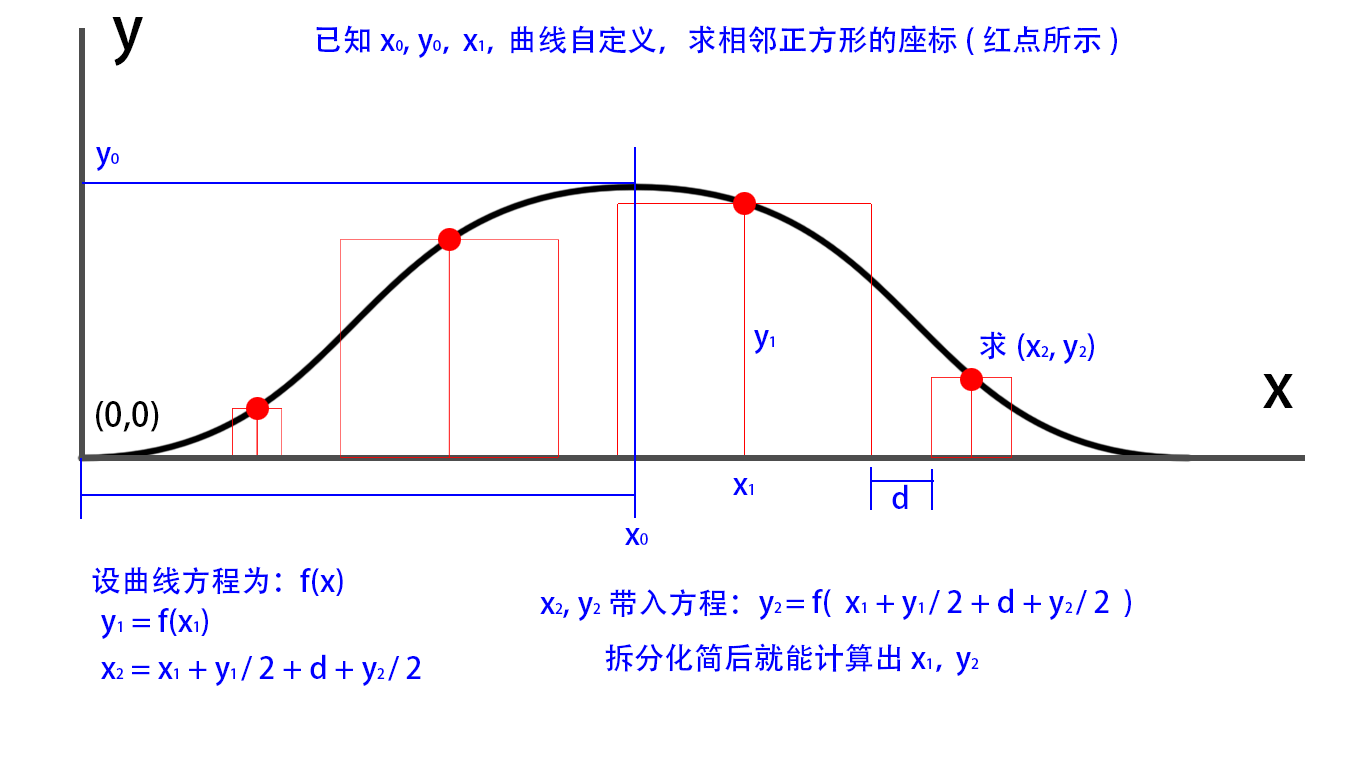
下图是我要求的东西，没有更多信息了

正方形是在曲线上移动的，只知道主正方形的 x 座标及间距 d
![img]( https://raw.githubusercontent.com/ZeronoFreya/Gallery/master/aa.png)

第 2 条附言 · 2022-03-04 15:44:05 +08:00

![img]( https://raw.githubusercontent.com/ZeronoFreya/Gallery/master/aa.png)

第 3 条附言 · 2022-03-04 15:45:05 +08:00

为啥图片不显示……

img

方程

请问

动画

14 条回复 • 2022-03-04 16:07:26 +08:00

czfy

2022-03-04 13:08:19 +08:00

这是正态分布？

a627667970

2022-03-04 13:09:02 +08:00

正态分布？

moen

2022-03-04 13:09:07 +08:00

这不就是贝塞尔曲线？

lujjjh

2022-03-04 13:15:04 +08:00

信息太少，推荐 https://easings.net/

yggd

2022-03-04 13:28:54 +08:00

贝塞尔曲线啊，控制点都给出了
https://javascript.info/bezier-curve

noe132

2022-03-04 13:33:04 +08:00

如果是标准的 cubic rezier
https://cubic-bezier.com/#.4,0,.6,1

const bezierEasing = require("bezier-easing")
const curve = bezierEasing(0.4, 0, 0.6, 1)
const xs = Array(11).fill(0).map((_, i) => i * 0.1)
const arr = xs.map(x => [x, curve(x)])
arr.forEach(pair => console.log(pair))

https://runkit.com/noe132/6221a3eec7c2b10008a4b158

mxT52CRuqR6o5

2022-03-04 13:33:11 +08:00 via Android

贝塞尔曲线+1

zeronofreya

2022-03-04 15:46:06 +08:00

@lujjjh 我更新了一下

zeronofreya

2022-03-04 15:46:23 +08:00

@czfy js 动画用的

zeronofreya

2022-03-04 15:48:20 +08:00

@noe132 我用这个库没法计算，不知道 x 的值，必须要曲线方程求解

thedrwu

2022-03-04 15:49:12 +08:00 via Android

exp(x*x/(x*x-c*c))
x 从-c 到+c

thedrwu

2022-03-04 15:51:55 +08:00 via Android

无限可微，边界所有导数都是 0
distribution 基函数的例子

misdake

2022-03-04 16:00:36 +08:00

2 个端点 2 个控制点的贝塞尔曲线，是 3 次的参数方程，给 x 解 y 的话，把三次方程求根公式搞进去，外部保证有唯一解，求出满足范围的实数解 t ，把 t 带入 y 的方程就能得到 y 。你现在的需求更复杂，自变量还有当前的 y ，很麻烦啊。
不要求精确解的话，不如直接二分法求 t ，再用 t 求 y 。

misdake

2022-03-04 16:07:26 +08:00

另外看你这个示意图，求的是一个斜率为 2 的直线和曲线的交点，如果 y0/x0 足够大，完全可能有 3 个解。